Theistic Science Group

Website at TheisticScience.com 

How Influx into the Natural Shows Itself in Physics:
a hypothesis

Ian Thompson

V2, Feb 29, 2020.

In my previous article in this issue, I list three area in physics which are not yet properly understood. These are (a) quantum gravity, (b) the need for tuning (fine-tuning, or renormalization) of parameters in quantum field theory, and (more generally) (c) the relation between mind and physics. Now I am going to propose a hypothesis for linking together (b) and (c), where influx from mind into physics occurs by local variations in the tuning of parameters that define quantum fields. Such variations could well be how influx from spiritual degrees shows itself in physics. This could be used to facilitate some of the molecular dynamical described by Hingorani (2014) and Smith (previous article).

In order to link fine-tuning in physics with spiritual influx, I propose that the highest degree in physics—the 3.1 degree—is where ‘ends’ are received in physics. By ends, I refer to what it is that determines the means or causes in physics, and what it is that manages or influences to basis parameters (masses and charge values) of the quantum fields. This is fine-tuning, in the sense that it occurs not just for the whole universe (in the Big Bang, for example), but locally. That is, this fine-tuning is different at each time, and in point in space. Thus this influx can be specific to living organisms, and can occur at all the needed scales and levels in psychology and biology, namely every day and every micros-second of our lives. But what is the mechanism of this? How would we detect it happening? How would we test this hypothesis?

SOMETHING VARIES IN PHYSICS

Our new idea is that the fine-tuned parameters of quantum field theory (masses and charges) can be varied locally in order to achieve ends in nature. This is not adding extra forces to nature, but rescaling the forces which already exist.  We will focus on the unit of electric charge . This value is built into the fine-structure constant  1/137. Some physicists  (Webb et al, 2001, 2011) have proposed varying  slowly over the age of the universe. Some kind of variation, therefore, is conceivable in physics. Now we propose to vary it over micro-seconds (millionths of a second), and within living organism. That is a new idea. 

The electric force  on charge q₁ at position r₁ from charge q₂ at position r₂ is

where  is a coefficient called the electric permittivity.  Clearly, varying a charge  will vary the force , and hence make make the charges move in different ways from previously.  Bekenstein (1982, 2002) showed that very similar effect to this can be obtained by varying the permittivity at the position of either charge ( or ) while keeping the charges constant. Now we have the force depending on  and  as

It is more helpful in physics to vary just , as charge conservation built into the Maxwell equations, the standard equations for electromagnetism. Maxwell’s equations do still allow  to to vary, as it does in dielectrics (as used in capacitors, etc.). But in our new application  is varied not just in dielectrics, but varies even in a vacuum. The speed of light depends on  by the equation , where  is the magnetic permeability. To keep Einstein happy with a constant speed of light, if the permittivity  varies, then  must vary inversely, to keep their product constant, and hence the speed of light constant too.

ENERGY CONSERVATION

For the spiritual to have effects in nature, and make a difference there, the physical laws of nature must be modified or extended. Many thinkers in centuries past have proposed physics extensions to allow minds to operate, but to keep energy conservation at the same time. They think this is a fundamental physical principle which should never be questioned, so they are really trying to keep the causal closure of physical nature. This is to keep a ‘closed shell’ around nature. Then actions of mind are limited to ideas of biased probabilities in quantum mechanics (Beck,  2008), or to varying time of the chance events (Stapp, 2006). But quantum chances affect very little in organisms. Others suggest that minds could move energy from one location to a nearby place but that does not conserve energy locally. Maybe non-local entanglement could be used, although it cannot be used for signals.

But now, in this symposium, we are trying to break that shell, and by means of new physical theory on the inside. Once the electric permittivity is that varies in time and space, that  fact alone means total energy and momentum are not conserved, by Noether’s theorem (Wikipedia, 2020a). Is that the end of the world? No! Is that the end of physics?  No! We can still do physics calculations using forces between objects  and  varying by a formula such as

For convenience, we will define  for new ‘variation’ functions  If , then there is no change from the standard vacuum.  The pairwise forces are now calculated as

METRIC TIME AND PROCESS TIME

We need to distinguish between "process time" and "metric time", since our project going to use each of these in separate ways.

Metric time is only in the natural, where it allows the numerical measurement of duration in time. Swedenborg always emphasizes this measure (metric) aspect of time in nature (DP 49, DLW 73, 161). It can well be regarded as the 4th dimension in space-time, along with 3D space dimensions. That dimension is ‘settled and constant’.

Process time is the sequences of changes of substance or state where-ever they may be. There is an order in process time, but only a counting order 1,2,3,.. , not an exact measurement (e.g 1.545867899). In fact, between any pair of events in process time, there is no limit to how many spiritual state changes can be inserted between them. So process time is not ‘settled and constant’.

Spiritual activities use process time, but no metric time. Whenever the desire or thought of an angel or mind changes, that is another step in process time.  One of Swedenborg’s main achievements was to describe process time in the spiritual world to eternity. The important feature for now is that planning can be done in spiritual or process time, since it involves thought in the mind. Physical activities use metric time in classical Newtonian physics.   But there is some process time in quantum physics as well, where it counts the actualization of propensities – changes of state even there.  

MAKING PLANS FOR DESIRED ENDS

We now need to discuss how the  would be varied to achieve desired ends in nature. How can plans be devised with ends in mind? Let’s try to make a proposal for physics that is correspondence with the way minds do their mental planning. Consider what the Writings tell us how love operates by means of wisdom, or correspondingly how desires operate by means of thinking and seeing to achieve its ends. I want to suggest there are successive steps in making any plan:

a)     Input of ends that are desired for a goal at some future time.

b)    foresight of the present up to that time to see what is already going to happen.

c)     Discerning the measure of goal match or mismatch

d)    A way to work on reducing mismatches, by thinking back to present starting point.

e)     A way to alter intermediate causes to make a plan that reduces the mismatch.

For example, in moving one’s arm to pick up a cup, we have:

a)     Desire to pick up a cup

b)    Imagine ahead to see where hand is going to be moving to

c)     Compare final hand position with cup position

d)    If see a possible mismatch, work backwards to present where the hand is now.

e)     Work out how arm muscles have to move to reduce mismatch, so hand can grasp cup.

In this article we want to find physical processes that are correspond to these five steps. Here ‘to correspond’ means to have functions organized in the same structure, but functions of different substances. Physical substances are made out of materials with no consciousness, no intentions, and no intelligence. Their function should be able to completely definable by mathematical laws, and hence able to be completely simulated on a computer. Instead of ends, for example, we will use the term ‘targets’, as they can be embodied in (say) thermostats or car cruise-controls without themselves being conscious or intelligent. What we are doing is re-introducing into natural science the concept of ‘final causes’ that was removed four hundred years ago. These targets, as final causes, will be in the highest discrete degree of nature, 3.1, in the physical ennead of my previous article:

           The physical ennead

PHYSICAL IMPLEMENTATION OF TARGETS

Step (a) in the mind is formulating a desire to do something, so in nature we have the first existence of a ‘target’.  By a ‘goal’ or ‘target’ or ‘end’ in the natural, I mean for example:

“How the molecules in the cell should be rearranged to achieve a use as an end.” We know that enzymes are protein molecule with a very special arrangement of atoms in order to make specific chemical reactions proceed much faster. But molecules are not produced in that arrangement, so they have to fold up in the required manner in order to be useful.

A target, therefore, could be the specific arrangements of a molecules at some future time ,
in order that the folded protein be catalyst or enzyme.   Defining such a target corresponds step (a) of making a plan.

The next step (b) requires some kind of foresight from the present  up to target time , to see first what is going to happen if no special action is taken. We are talking of the ‘near future’ in metric time, where no changes of state (in ‘process time’) have yet occurred. In order to work towards a target for a folded molecule in a cell, the organism must ’know’ whether it is ‘on track’, or not. It must be able to extrapolate from present to target time, but have to do so without any consciousness, because this in physical nature, which is nothing spiritual. I propose that the cell uses the 3.2-degree electromagnetic fields extrapolated to the needed future time. These fields are deterministic by Maxwell’s equations, and have little quantum chance if considered in quantum field theory. In either formalism, the extrapolated field should be a reliable indicator of what would happen soon, given the present physical state of affairs. Thus, the 3.2 degree contributes to step (b) of making a plan.

The third step (c) is to make a measure of goal match or mismatch. This corresponds to discrimination in the understanding about the difference between two arrangements of molecules, namely the target configuration compared with the configuration extrapolated from the present state.  This is the task of the target itself, as it sits in the 3.1.3 degree above the configurations of fields in the 3.2.3 agree. Having arranged a target, that sub-degree provides feedback to how close the present future is to achieving the target. We can formulate this mathematically in terms of a function   which gives the difference to target, as  =  (extrapolation(T_g) — target)².  So mathematically, the goal is to minimize .

If  is zero or very small, then nothing else needs to be done in step (d). But if it is large, and indicates a significant ‘miss’ of the target, then something needs to be done to improve the situation. Mentally, we often work back from an imagined goal, to see all the steps needed to get there. I am now going to hypothesize that something similar happens with physical targets.  For this purpose, it makes sense to use adjoint solutions, which are the solutions of the same equations for waves and forces, but backwards in time. Adjoint solutions are often used in design problems in engineering, to find the sensitivities to all input parameters of an overall performance measure (see e.g. Wikipedia, 2019).  So here, we would use the time-reversed solution of Maxwell’s equations (for electromagnetic waves) and of Newton equations (for particles) from  back to the present time . These solutions start with magnitude given by the current target measure . And then the overlap of the forward and adjoint solutions gives the partial derivatives , showing the sensitivities for how the goal  varies with permittivity variation functions . This is a ‘back-propagation method’ common in computer model: see Wikipedia (2020b).

Finally, step (e) needs a way to find changes to cause variations , to reduce the mismatch .

The simplest method to use in a physical system is the ‘gradient descent method’. This method is, for some speed coefficient , to change all the  by increments

Then, after each change of , have to recalculate forward and adjoint solution. The method is to iterate above steps of incrementing and recalculating, until  is small enough. That is the way to attain the target.

NUMERICAL DEMONSTRATIONS OF PRINCIPLE

In order to demonstrate that the above method works in principle, I have calculated the behavior and response of a simple 100-particle polypeptide molecule inside a chaperonin cage made of 2 rings, each ring of 8 negative charges of .  The molecule has dynamical bond lengths and angles with their own spring constants, and the particles have mixtures of charges  and . A standard Molecular Dynamics method is used to calculate the trajectory and velocity vectors , for each particle  using standard Newtonian mechanics. There is a generic repulsive cage wall to keep the molecule confined, and there is no water.

The target is give as : the desired position for each particle at some later time  The goal function is  which gives difference to target, namely  =  .  The goal is thus to minimize, preferably to =0. This is accomplished by adjusting the permittivities, or dielectric ‘constants’ by their variation functions . This controls the effectiveness of charges in attracting or repelling, both for the charges on the molecule, and for the charges on the cage wall.

Numerical examples successfully show that it is possible to move the molecule, say one 1 nm to the left within the cage. Fig 2 below (left) shows how the  function decreases to near zero after 10 or 15 iterations of the back-propagation method.

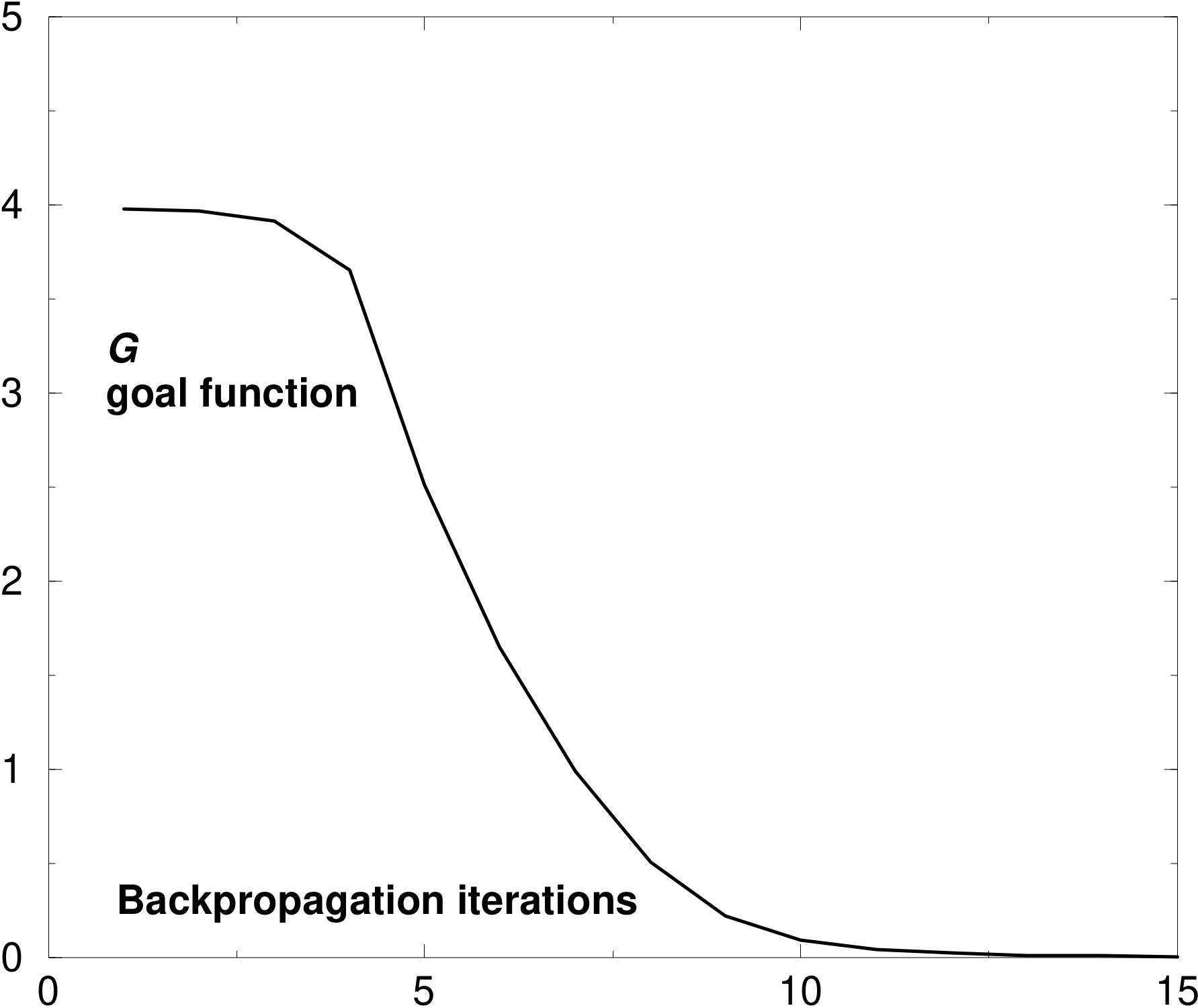
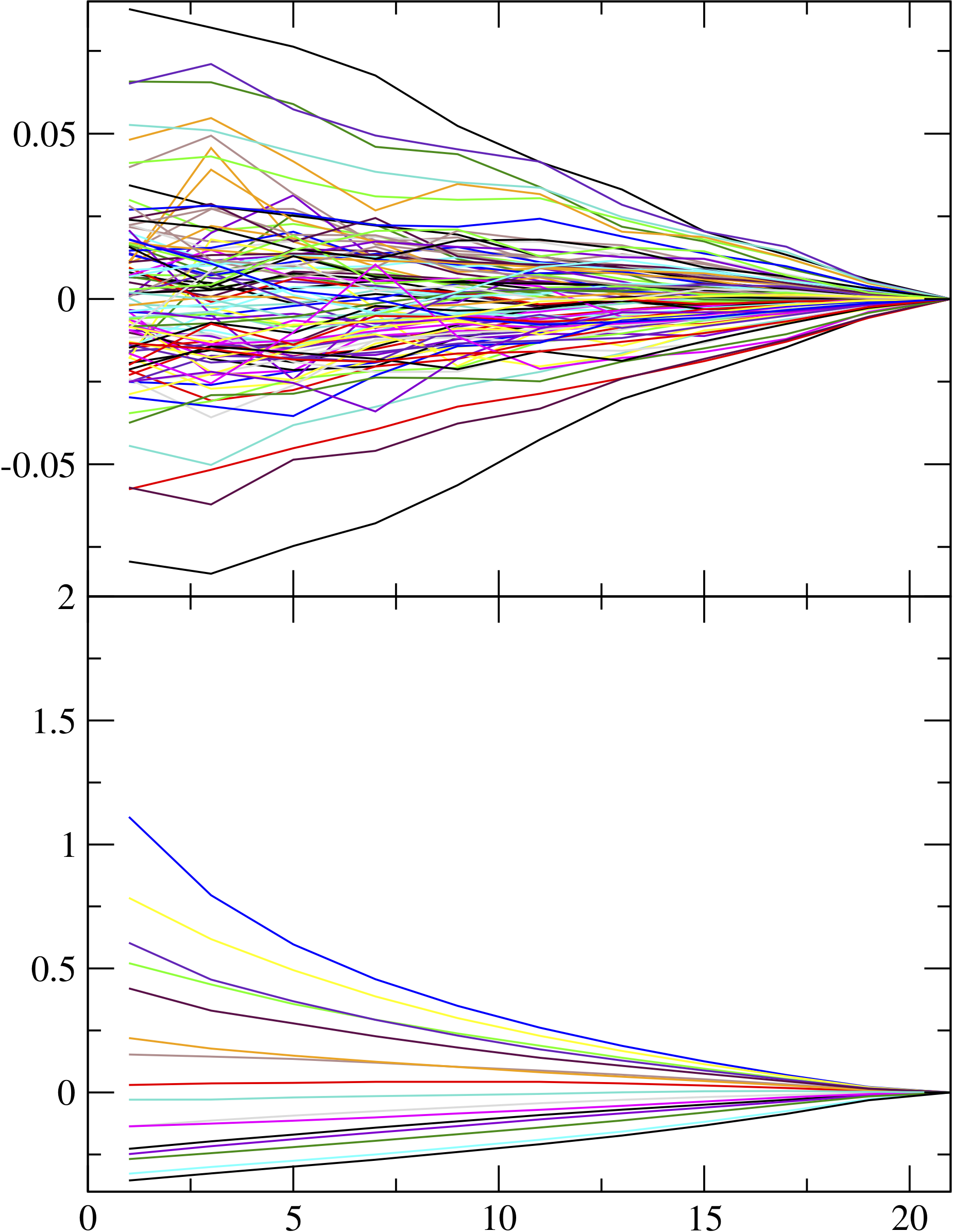
Fig. 2 (right) shows how much the variation functions  had to be to achieve that goal. The upper plot show variation for the 100 molecule charges, and the lower plot shows the needed variations for the 16 charges on the cage wall. A few of them have large increases to start with.

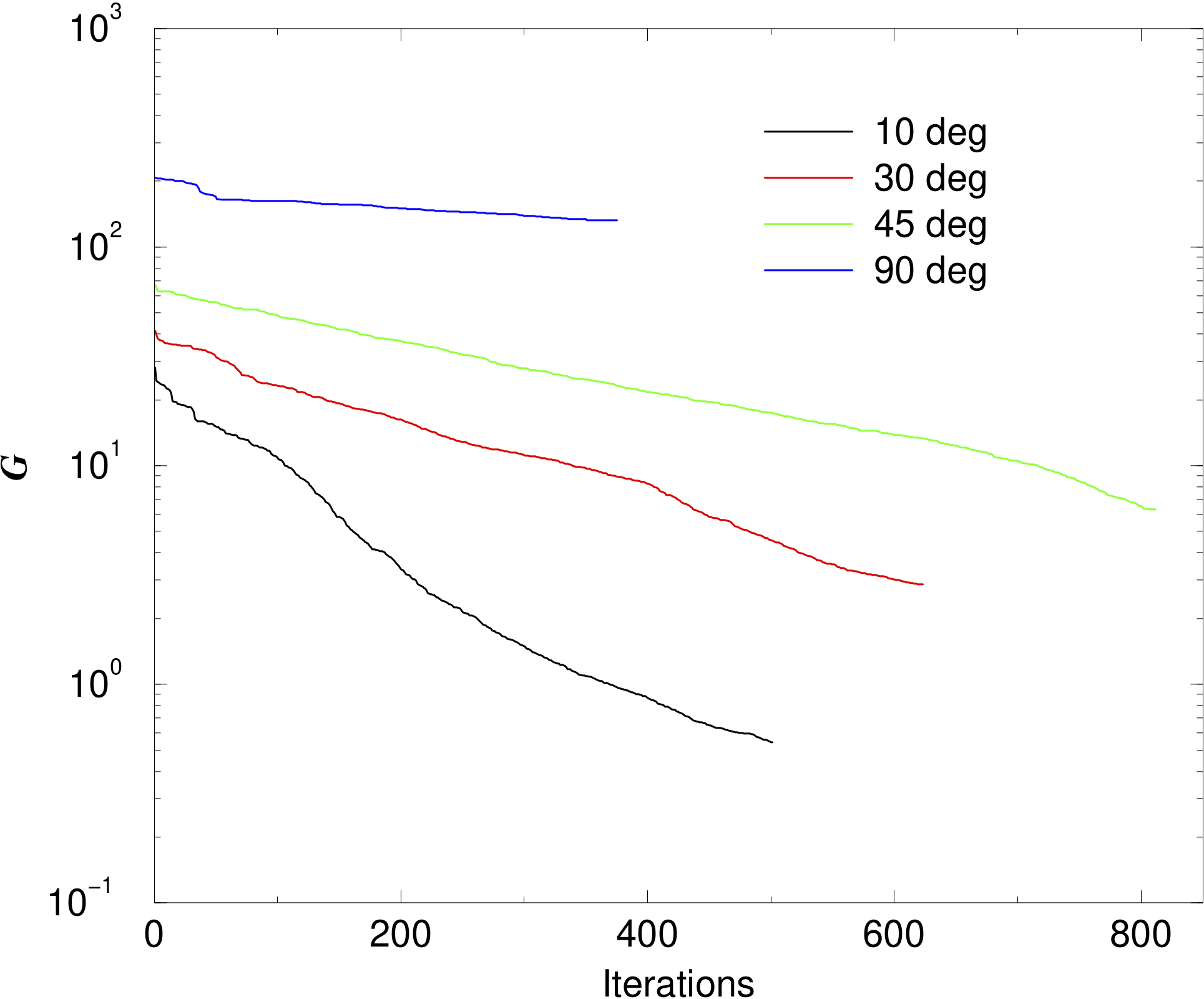
A second demonstration seeks to rotate a molecule in place, by some number of degrees.  This is tried for angles  10 , 3045, 90. The Fig. 3 below shows how quickly the  function decreases (or not) as iterations proceed. The method seems to fail for 90, and is slow for 45 rotations. The method has to fail for 180 , as then it is stuck between going to the left and to the right, like Buridan’s ass.

A final simple example was how to reshape part of a molecule from one configuration to another.  Descriptions and videos are available on line at Thompson (2019).

CONCLUSIONS

We may conclude that it can be done for a physical method to achieve goals specified by influx from higher discrete degrees.  I find that simple targets are easy to reach, especially if there is zero or small energy change. More complicated reshaping can also be done, but often fail by moving very slowly when part way through. It appears that the function has ‘local minima’ just like energy does. Furthermore, convergence (is difficult at higher temperatures, as then thermal fluctuations produce many local minima with narrow barriers between them.

Future improved calculations could try to implement sequences of targets following each other. We note that this method is not itself ‘intelligent’ at all. Another improvement in physical realism would be to put in the water molecules, and to try for convergence at higher temperatures. At the moment convergence in those cases should ideally be helped by fast fluctuations in , maybe even fast enough to match the thermal vibrations? And we should before long try ‘all atom’ calculations, not just amino acid ‘particles’. We also need more realistic hydrogen bonds, and to constrain dihedral angles.

Now, still, we can begin to answer the question in my title: namely how influx into the natural shows itself in physics. We can propose two hypotheses to answer that question. First, concerning what influx changes in physics, we can suggest that it is the relative permittivity of the vacuum. Second, concerning how influx changes could be used in physics, the answer could be that, for target configurations given by influx into the natural, there is a physical feedback mechanism to bring physical objects closer to this target in the near future.

This project presents several achievements. It makes a proposal for how ‘spiritual influx’ could have effects in nature. Furthermore, these effects on permittivity should be measurable in biophysics experiments.  With this proposal, we see after some centuries how ‘final causes’ could once again seen to be active in nature. This is by bringing the physical future into line with a target, and doing so without time travel and without altering the historical past. Thus we can imagine how the physical universe is no longer ‘causally closed’, and that a much greater range of scientific explanations should be possible including those in line with a theistic science inspired by the Writings.

REFERENCES

Beck F. (2008). Synaptic quantum tunnelling in brain activity. NeuroQuantology, 6 (2). http://www.neuroquantology.com/index.php/journal/article/viewArticle/168

Bekenstein, J.D. (1982) Fine Structure Constant: Is It Really a Constant? Phys Rev, D25, 1527. https://link.aps.org/doi/10.1103/PhysRevD.25.1527

Bekenstein, J.D. (2002) Fine-structure constant variability, equivalence principle, and cosmology. Phys Rev D, 66, 884.  https://link.aps.org/doi/10.1103/PhysRevD.66.123514

Hingorani, K.S. (2014), Gierasch, L.M. Comparing protein folding in vitro and in vivo: foldability meets the fitness challenge. Current Opinion in Structural Biology, 24, 81. https://linkinghub.elsevier.com/retrieve/pii/S0959440X13002017

Stapp, H.P.  (2006) Quantum Interactive Dualism: An Alternative T=to Materialism. Zygon,  41 (3) pp. 599-616. https://onlinelibrary.wiley.com/doi/full/10.1111/j.1467-9744.2005.00762.x

Thompson, I.J. (2019), A hypothesis for How Influx into the Natural Shows Itself in Physics, Talk at Bryn Athyn College, Oct 12, 2019. Slides with videos online at http://www.theisticscience.com/talks.htm#ian2 .

Webb, J.K. (2001), M T Murphy, V V Flambaum, V A Dzuba, J D Barrow, C W Churchill, J X Prochaska, and A M Wolfe, Further Evidence for Cosmological Evolution of the Fine Structure Constant, Phys Rev Lett, 87, 205-4. https://link.aps.org/doi/10.1103/PhysRevLett.87.091301

Webb, J. K. (2011), King, J. A., Murphy, M. T. and Flambaum, V. V. and Carswell, R. F. and Bainbridge, M. B., Indications of a Spatial Variation of the Fine Structure Constant, Phys. Rev. Lett. 107, 191101. https://doi.org/10.1103/PhysRevLett.107.191101

Wikipedia (2019): Adjoint State Method. https://en.wikipedia.org/wiki/Adjoint_state_method

Wikipedia (2020a): Noether’s Theorem, https://en.wikipedia.org/wiki/Noether%27s_theorem

Wikipedia (2020b): Back-propagation. https://en.wikipedia.org/wiki/Backpropagation